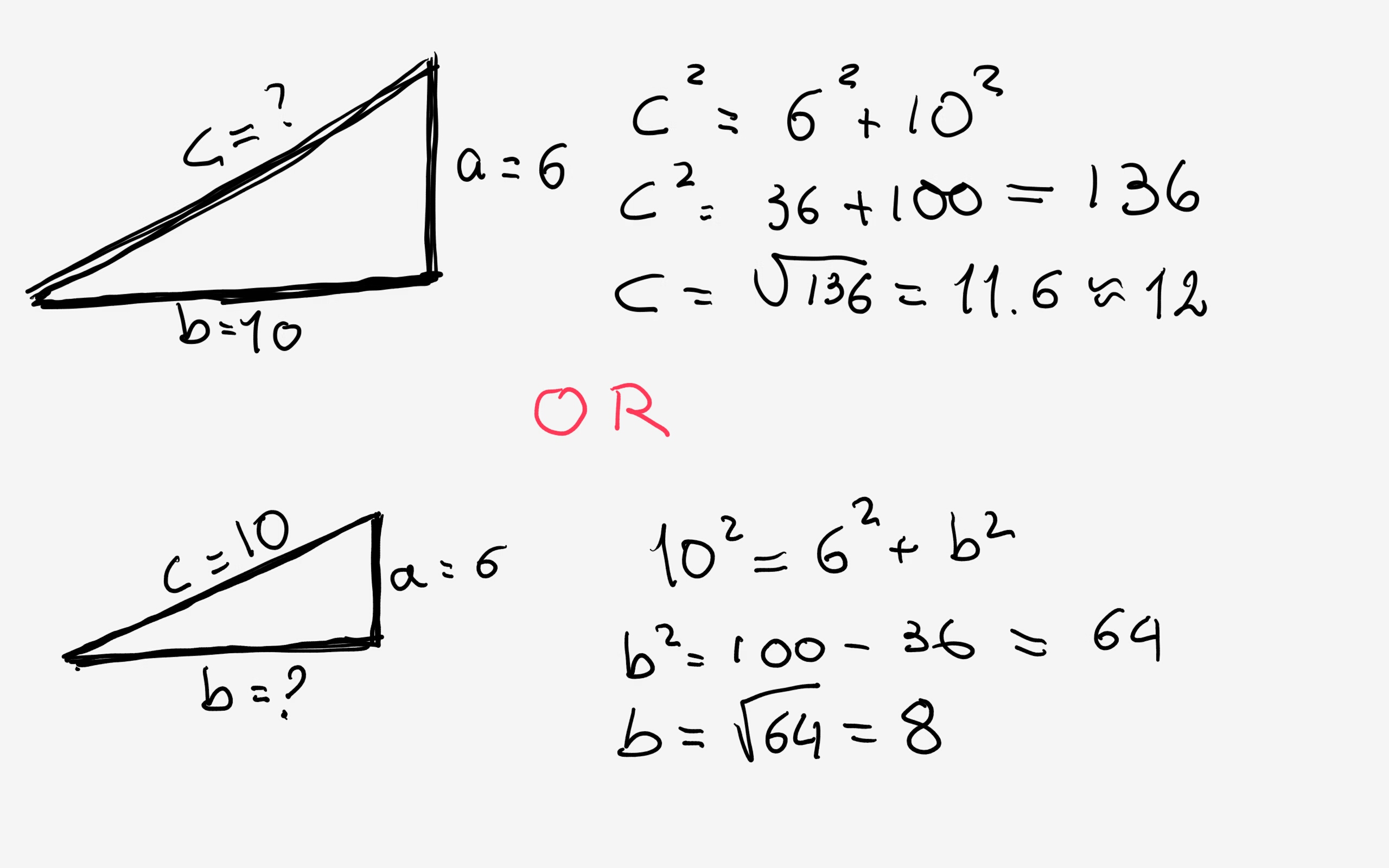
How To Find A Right Triangle Using Pythagorean Theorem Perpendicular2 + base2 = hypotenuse2
Here are two more Pythagorean Triples: 5, 12, 13. 9, 40, 41. 5 2 + 12 2 = 13 2. 9 2 + 40 2 = 41 2. 25 + 144 = 169.

Premium AI Image An artistic interpretation of a portrait of Pythagoras the renowned ancient
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths.. If C is chosen as a starting point, the sequence is: C, G, D, A, E, B, F♯, C♯, A♭, E♭, B♭, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another.

Tren Gaya 24+ Rumus Tripel Pythagoras
This is the first of two articles on right-angled triangles whose sides have lengths that are whole numbers. The second article is called "Pythagorean Triples II".Both of these articles can be read in conjunction with the article "Picturing Pythagorean Triples ".The whole numbers a, b, c are a Pythagorean triple if a and b are the lengths of the two sides of a right-angled triangle with.
When To Use Pythagoras Cosine Rule Or The Sine Rule
Pythagorean triples are a2+b2 = c2 where a, b and c are the three positive integers. These triples are represented as (a,b,c). Here, a is the perpendicular, b is the base and c is the hypotenuse of the right-angled triangle. The most known and smallest triplets are (3,4,5). Learn Pythagoras theorem for more details.
Triple Pythagorean Triples MooMooMath and Science
Rumus Phytagoras, Contoh Soal dan Cara Mengerjakannya. Soal segitiga dengan sudut penyiku yang sama dapat dikerjakan dengan rumus phytagoras. Biasanya kedua sisi telah diketahui terlebih dahulu. Rumus phytagoras merupakan formula untuk mencari salah satu sisi dalam segitiga siku-siku. Awalnya rumus ini digunakan untuk mencari sisi miring dalam.
How do you use the Pythagorean Theorem to determine if the following triangle with sides a, b
The Pythagorean triple definition says it is a set of three positive integers a, b, c that satisfy the relationship:. a² + b² = c². If you have already learned about the Pythagorean theorem, you surely recognize this formula. Three integers constitute a Pythagorean triple if they are the sides of a right triangle: c is the hypotenuse (the longest side of the triangle), while a and b are the.

teorema pythagoras , matematika kelas 8 bse k13 rev 2017 ,lat 6,1 no 5 menentukan x YouTube
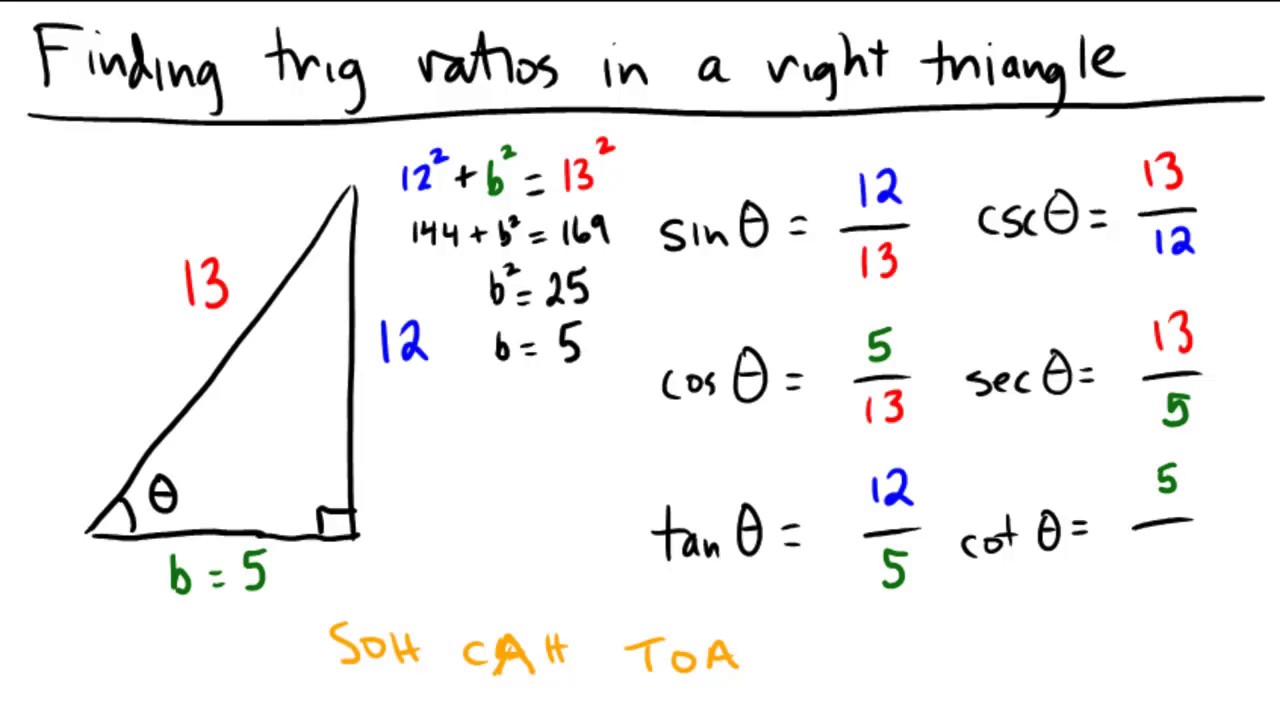
The hypotenuse formula simply takes the Pythagorean theorem and solves for the hypotenuse, c.To solve for the hypotenuse, we simply take the square root of both sides of the equation a² + b² = c² and solve for c.When doing so, we get c = √(a² + b²).This is just a reformulation of the Pythagorean theorem and is often associated with the name hypotenuse formula.
An Introduction To Pythagoras Theorem SyedLearns
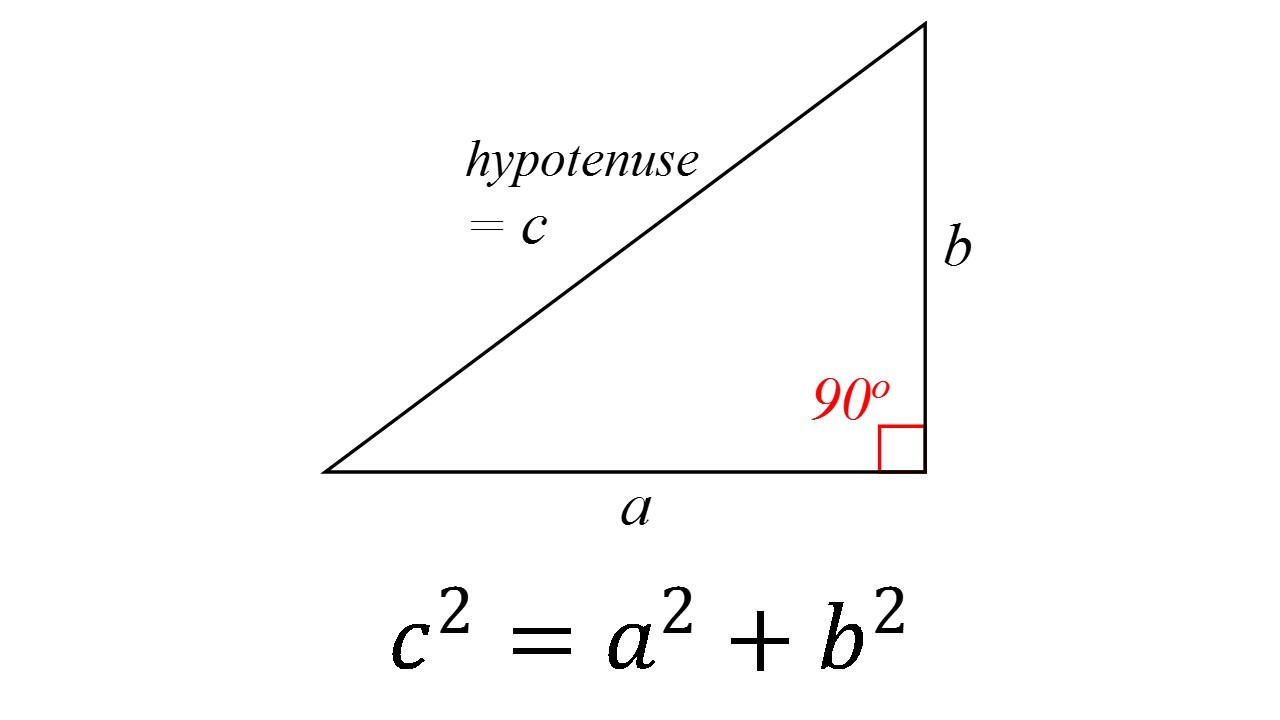
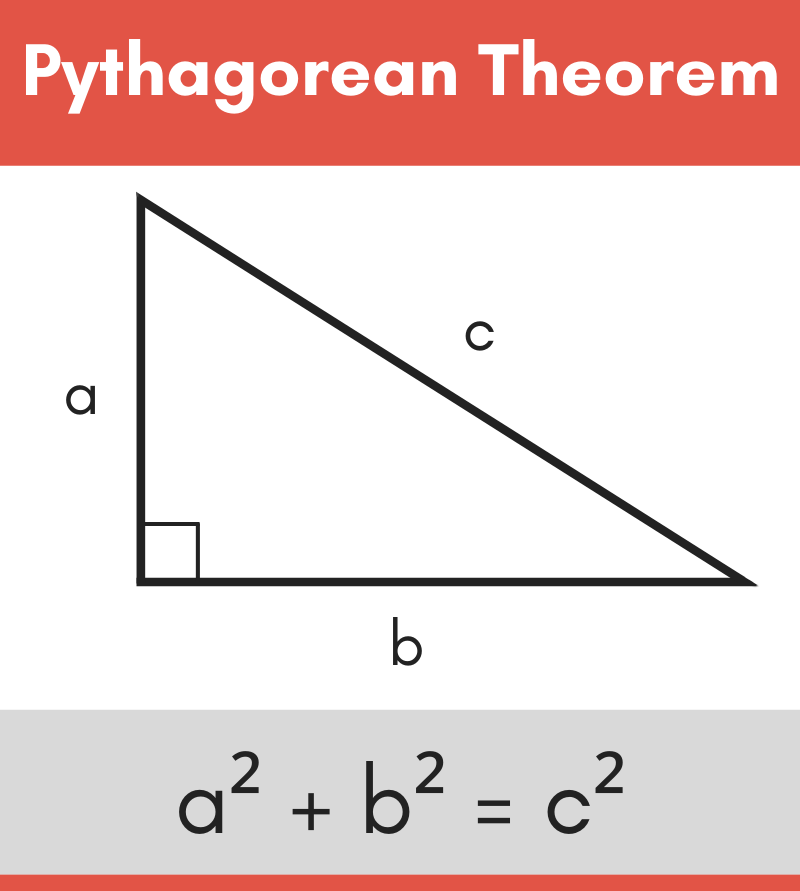
Pythagorean theorem. The sum of the areas of the two squares on the legs ( a and b) equals the area of the square on the hypotenuse ( c ). In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle.

Pembuktian Teorema Phytagoras Bagian Kedua yudienamaku
Pythagoras of Samos (Ancient Greek: Πυθαγόρας ὁ Σάμιος, romanized: Pythagóras ho Sámios, lit. 'Pythagoras the Samian', or simply Πυθαγόρας; Πυθαγόρης in Ionian Greek; c. 570 - c. 495 BC) was an ancient Ionian Greek philosopher, polymath and the eponymous founder of Pythagoreanism.His political and religious teachings were well known in Magna Graecia and.

Pythagoras 51213 Triangle. GCSE 91 Maths Edexcel June 2017 Paper 1H Q5 YouTube
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A triangle whose sides form a Pythagorean triple is called a Pythagorean.
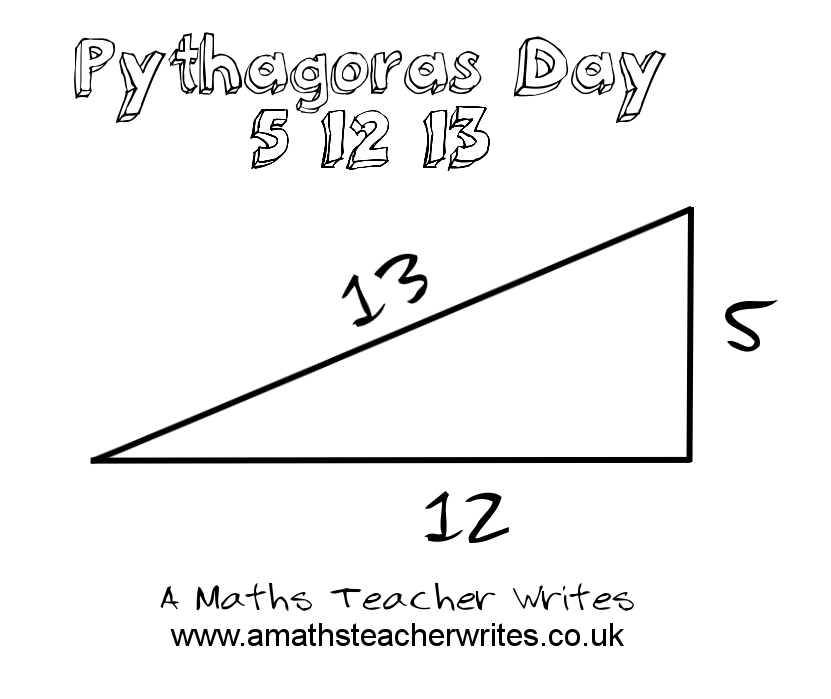
Pythagoras Day
Pythagorea Level 13.12: Construct all triangles whose vertices. are nodes (one of them is in the point. A) and with sides of length root 13, 2 root 5, and root 37. If you have any doubt regarding Pythagorea answers given here you can watch video below or you can comment on this post-. ← Pythagorea Level 13.11 Answer Solution.

Primitive Pythagorean Triples Formula banhtrungthukinhdo2014
Pythagorean Triples - Advanced (You may like to read Pythagoras' Theorem and Introduction to Pythagorean Triples first). A "Pythagorean Triple" is a set of positive integers a, b and c that fits the rule:. a 2 + b 2 = c 2. Triangles. And when we make a triangle with sides a, b and c it will be a right angled triangle (see Pythagoras' Theorem for more details):

MEDIAN Don Steward mathematics teaching pythagorean triples introduction
c2 = a2 + b2 atau c = √a2 + b2. a2 = c2 - b2 atau a = √c2 - b2. b2 = c2 - a2 atau b = √c2 - a2. Ketiga rumus di atas bisa kamu gunakan untuk menghitung berbagai sisi dari segitiga siku siku. Berikut ini merupakan beberapa triple pythagoras. 3, 4, 5.

Pythagorean Triples Formula What Is Pythagorean Triples Formula? Examples
The Pythagorean Triples here are also called Primitive Pythagorean Triples because the Greatest Common Divisor ( GCD) or the Greatest Common Factor ( GCF) of the three positive integers is equal to 1. where the GCD of [latex]a,b,c [/latex] equals [latex]1 [/latex]. It also implies that [latex]a,b [/latex] and [latex]c [/latex] are relatively.

Teorema Phytagoras Serta Contoh Soal Tambah Pinter
Pythagorean Triples - Explanation & Examples What is a Pythagorean triple? Pythagorean triple (PT) can be defined as a set of three positive whole numbers that perfectly satisfy the Pythagorean theorem: a 2 + b 2 = c 2.. This set of numbers are usually the three side lengths of a right triangle.

The Golden verses of Pythagoras Fabre d'Olivet, Antoine, 17671825 Free Download, Borrow
According to the definition, the Pythagoras Theorem formula is given as: Hypotenuse2 = Perpendicular2 + Base2. c2 = a2 + b2. The side opposite to the right angle (90°) is the longest side (known as Hypotenuse) because the side opposite to the greatest angle is the longest. Consider three squares of sides a, b, c mounted on the three sides of a.